
Hace ya varios meses me decidí a despertar este blog, pero la verdad es no esoy cumpliendo con ello. Sigue estando aletargado. Pero a veces, ocurren cosas que lo hacen despertar.
Soy un seguidor de la terna Arrow, The Flash y Legends of Tomorrow. Para ver estas series hay que tener bastante suspensión de la incredulidad. Sobre todo con Legends of Tomorrow, que está superando a Doctor Who en cuanto a incoherencias con viajes en el tiempo. Pero hay cosas que directamente no tienen ningún sentido, y van más allá de lo absurdo.
Eso pasó en el episodio de Arrow de hace unas semanas, que formaba parte del crossover llamado «Invasion!» (basado en el evento con mismo nombre que ocurrió en los cómics DC, a finales de los 80). No, no voy a hablar de superpoderes, ni de alienígenas, ni de viajes en el tiempo, ni de magia, ni de tecnología imposible. No. Lo que voy a comentar es algo muy sencillo, pero que supera todo.
Veréis, al final del episodio de The Flash, Oliver y compañía (es decir, Green Arrow y algunos compañeros) son abducidos por los dominadores (los alienígenas que atacan la Tierra) mediante alguna tecnología teletransportadora, a lo Star Trek. En el episodio de Arrow, Felicity y Cisco ponen sus cabezas a trabajar para averiguar dónde los tienen. No voy a entrar en cómo lo hacen, que es una mezcla de entender tecnología alienígena nunca vista y algo de esoterismo. Os reproduzco el siguiente diálogo:
FELICITY: La señal viene de... no es posible. Latitud -3.127, longitud -23.7987.
CISCO: Pero eso no tiene ningún sentido. Las coordenadas geográficas no tienen números negativos.
FELICITY: Quiero decir, las tienen. Sólo cuando... ¡Oh, Dios mío! Creo que sé dónde están.
Y entonces hay un corte que nos muestra a Oliver y sus amigos (tras intentar escapar), mirando perplejos el espacio exterior, dentro de una nave alienígena.
Recapitulemos por si alguien se ha perdido. Según los guionistas de Arrow, las coordenadas geográficas tienen valores positivos en la Tierra, y negativos en el espacio. Sí. Así como lo estáis leyendo.
Bueno, vamos a repasar lo que nos enseñaron en el colegio sobre las coordenadas geográficas. Para ello, debemos recordar que la Tierra tiene una forma más o menos esférica (aunque ya sabemos que no es una esfera perfecta). Eso quiere decir que cualquier punto de su superficie puede representarse mediante dos coordenadas, siendo cada una de ellas un ángulo con respecto a un plano fijo.

Pues bien. La latitud de un punto es el ángulo que forma dicho punto con el ecuador, expresado en grados. Eso quiere decir que todos los puntos del ecuador tienen latitud cero, y que los polos tienen latitud 90. Obviamente, necesitamos indicar si el ángulo es hacia el norte o hacia el sur. Por convenio se considera que hacia el norte la latitud es positiva, y hacia el sur, negativa. Eso quiere decir que la latitud del polo sur es -90.
Por otro lado, la longitud de un punto es el ángulo que forma dicho punto con el meridiano cero. Dicho meridiano es una línea de norte a sur, que establecemos como referencia. En la actualidad, como muchos sabréis, se usa el meridiano de Greenwich, llamado así porque pasa por el antiguo observatorio astronómico de Greenwich, Londres. Al igual que con la latitud, necesitamos indicar el sentido del ángulo, es decir, hacia el este o hacia el oeste del meridiano. Por convenio, se considera el este como positivo y el oeste como negativo.
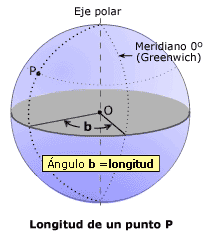
Como podéis ver, las coordenadas geográficas pueden tener perfectamente valores negativos. Es algo normal. Es más, como habréis podido deducir, sólo una cuarta parte de la superficie terrestre tiene coordenadas geográficas positivas. El resto, tiene al menos una coordenada negativa. Por curiosidad, si vais a Google Maps y ponéis en la caja de búsqueda «-3.127, -23.7987» veréis que las coordenadas corresponden a un punto en el Oceano Atlántico.
Fijaos que en ningún momento he mencionado la altura. Eso es porque la latitud y longitud son coordenadas para situar un punto en una superficie esférica. Son bidimensionales (obvio, pues son dos valores). Unas mismas coordenadas pueden corresponder con varios puntos distintos, todos ellos en la misma vertical (de hecho, corresponde a todos los infinitos puntos de dicha vertical). Pensad por ejemplo en un edificio de varias plantas. Si pensamos que los pisos están distribuidos de la misma forma, la puerta de entrada de cada planta, por ejemplo, tendrá las mismas coordenadas en cada una. Por tanto, no tiene ningún sentido que unas coordenadas geográficas indiquen un punto en el espacio. En todo caso, representarían la proyección de dicho punto en la superficie terrestre, con lo que no serviría de mucho.
Así que como veis, el que unas coordenadas geográficas negativas indiquen un punto en el espacio exterior, es algo totalmente absurdo. No tiene ni pies ni cabeza. Y no, no vale eso de que «es una serie de ciencia ficción». Eso vale para los alienígenas, superpoderes, viajes en el tiempo y demás. Pero no para cambiar un sistema de coordenadas definido.
